Theorems

From MHSHS Wiki

(Difference between revisions)
Jump to: navigation, search
(→Vertical Angle Theorem)
(→Vertical Angle Theorem)
Line 43: Line 43:
==Vertical Angle Theorem==
==Vertical Angle Theorem==
 +
===Vertical angles are equal===
Look at the intersecting line segments EF & GH below. We know that <math>\angle 1 + \angle 2 = 180^\circ</math> since they're supplementary angles. We also know that <math>\angle 1 + \angle 4 = 180^\circ</math> because they too are supplementary. If that's the case, it must be true that <math>\angle 2 = \angle 4</math> by substitution.  
Look at the intersecting line segments EF & GH below. We know that <math>\angle 1 + \angle 2 = 180^\circ</math> since they're supplementary angles. We also know that <math>\angle 1 + \angle 4 = 180^\circ</math> because they too are supplementary. If that's the case, it must be true that <math>\angle 2 = \angle 4</math> by substitution.  
-
By the same logic, <math>\angle 1 = \angle 3</math>
+
By the same logic, <math>\angle 1 = \angle 3</math>. Angle 2 and angle 4 are vertical angles, and angle 1 and angle 3 are also vertical angles.
[[File:Vertical_angles.gif|Vertical angles]]
[[File:Vertical_angles.gif|Vertical angles]]

Revision as of 01:18, 21 October 2009

Contents

The Distance Formula

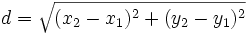
d=\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}

Example: Find the distance between point A(5,-7) and B(-6,-2) and leave your answer in radical form.

Solution: Let A be point 1 and B be point 2. We have 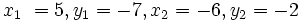x_1\ =5,y_1 = -7, x_2 = -6, y_2 = -2

Substituting we have 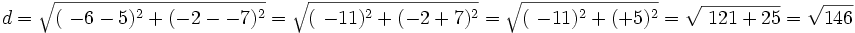d=\sqrt{(\ -6 -5)^2 + (-2 - -7)^2} = \sqrt{(\ -11)^2 + (-2 +7)^2} = \sqrt{(\ -11)^2 + (+5)^2} = \sqrt{\ 121 + 25} = \sqrt{146}

Try some distance problems at Distance & Midpoint 9-2 ME Worksheet

Sum of the Sides of a Triangle

Thm: The sum of two sides of any triangle must be greater than the third side

Example: Given two sides of a triangle are 8 inches and 11 inches, find all the possible lengths of the third side (also known as S3)

Solution: Since we know that 8 + 11 must be greater than S3, we have 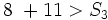8\ + 11 > S_3, so S3 must be less than 19. But what is the smallest value that S3 can be?


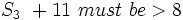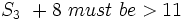Well, we know that S_3\ + 11\ must\ be > 8 , but 11 is already greater than 8 so that doesn't help us. However we also know that S_3\ + 8\ must\ be > 11 .

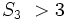Using algebra we subtract 8 from both sides of our inequality we get S_3\ + 8 {\color{Red}-8}\ > 11 {\color{Red}-8} , so S_3\ > 3. Our final answer is 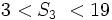3 < S_3\ < 19 (our third side must be greater than 3 but less than 19).

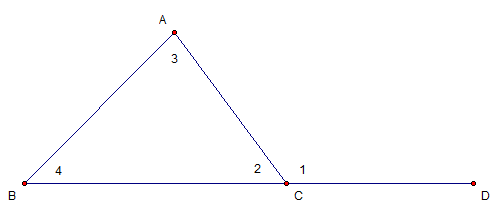
External Angle Theorem

Thm: An external angle is equal to the sum of the two opposite interior angles.

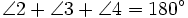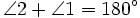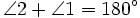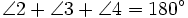Look at the figure below. We know that the sum of the interior angles of a triangle is 180 degrees. That means that in triangle ABC below, \angle 2 + \angle 3 + \angle 4 = 180^\circ. We also know that angles 1 and 2 are supplementary angles, meaning that \angle 2 + \angle 1 = 180^\circ. So if \angle 2 + \angle 1 = 180^\circ and \angle 2 + \angle 3 + \angle 4 = 180^\circ, then it must be true that 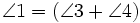\angle 1 = (\angle 3 + \angle 4) by substitution.


caption

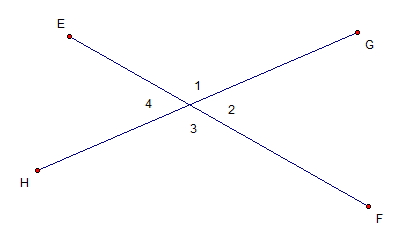
Vertical Angle Theorem

Vertical angles are equal

Look at the intersecting line segments EF & GH below. We know that 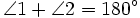\angle 1 + \angle 2 = 180^\circ since they're supplementary angles. We also know that 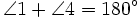\angle 1 + \angle 4 = 180^\circ because they too are supplementary. If that's the case, it must be true that 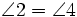\angle 2 = \angle 4 by substitution. By the same logic, 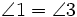\angle 1 = \angle 3. Angle 2 and angle 4 are vertical angles, and angle 1 and angle 3 are also vertical angles.

Vertical angles

Supplementary Angle Theorem

Complementary Angle Theorem

The Sum of the Interior Angles of a Triangle

External Angle Theorem

SAS - SSS Triangle Congruence Theorems

The Sum of the Interior Angles of any Polygon

The Measure of Each Interior Angle of a Regular Polygon

The Measure of Each Exterior Angle of a Regular Polygon

The Sum of the Exterior Angles of any Polygon

Retrieved from "http://wiki.mhshs.org/index.php/Theorems"
Personal tools
Resource Types